All posts tagged Euclid

The Book of Universes by John D. Barrow (2011)

This book is twice as long and half as good as Barrow’s earlier primer, The Origin of the Universe.

In that short book Barrow focused on the key ideas of modern cosmology – introducing them to us in ascending order of complexity, and as simply as possible. He managed to make mind-boggling ideas and demanding physics very accessible.

This book – although it presumably has the merit of being more up to date (published in 2011 as against 1994) – is an expansion of the earlier one, an attempt to be much more comprehensive, but which, in the process, tends to make the whole subject more confusing.

The basic premise of both books is that, since Einstein’s theory of relativity was developed in the 1910s, cosmologists and astronomers and astrophysicists have:

  1. shown that the mathematical formulae in which Einstein’s theories are described need not be restricted to the universe as it has traditionally been conceived; in fact they can apply just as effectively to a wide variety of theoretical universes – and the professionals have, for the past hundred years, developed a bewildering array of possible universes to test Einstein’s insights to the limit
  2. made a series of discoveries about our actual universe, the most important of which is that a) it is expanding b) it probably originated in a big bang about 14 billion years ago, and c) in the first few milliseconds after the bang it probably underwent a period of super-accelerated expansion known as the ‘inflation’ which may, or may not, have introduced all kinds of irregularities into ‘our’ universe, and may even have created a multitude of other universes, of which ours is just one

If you combine a hundred years of theorising with a hundred years of observations, you come up with thousands of theories and models.

In The Origin of the Universe Barrow stuck to the core story, explaining just as much of each theory as is necessary to help the reader – if not understand – then at least grasp their significance. I can write the paragraphs above because of the clarity with which The Origin of the Universe explained it.

In The Book of Universes, on the other hand, Barrow’s aim is much more comprehensive and digressive. He is setting out to list and describe every single model and theory of the universe which has been created in the past century.

He introduces the description of each model with a thumbnail sketch of its inventor. This ought to help, but it doesn’t because the inventors generally turn out to be polymaths who also made major contributions to all kinds of other areas of science. Being told a list of Paul Dirac’s other major contributions to 20th century science is not a good way for preparing your mind to then try and understand his one intervention on universe-modelling (which turned, in any case, out to be impractical and lead nowhere).

Another drawback of the ‘comprehensive’ approach is that a lot of these models have been rejected or barely saw the light of day before being disproved or – more complicatedly – were initially disproved but contained aspects or insights which turned out to be useful forty years later, and were subsequently recycled into revised models. It gets a bit challenging to try and hold all this in your mind.

In The Origin of the Universe Barrow sticks to what you could call the canonical line of models, each of which represented the central line of speculation, even if some ended up being disproved (like Hoyle and Gold and Bondi’s model of the steady state universe). Given that all of this material is pretty mind-bending, and some of it can only be described in advanced mathematical formulae, less is definitely more. I found The Book of Universes simply had too many universes, explained too quickly, and lost amid a lot of biographical bumpf summarising people’s careers or who knew who or contributed to who’s theory. Too much information.

One last drawback of the comprehensive approach is that quite important points – which are given space to breathe and sink in in The Origin of the Universe are lost in the flood of facts in The Book of Universes.

I’m particularly thinking of Einstein’s notion of the cosmological constant which was not strictly necessary to his formulations of relativity, but which Einstein invented and put into them solely in order to counteract the force of gravity and ensure his equations reflected the commonly held view that the universe was in a permanent steady state.

This was a mistake and Einstein is often quoted as admitting it was the biggest mistake of his career. In 1965 scientists discovered the cosmic background radiation which proved that the universe began in an inconceivably intense explosion, that the universe was therefore expanding and that the explosive, outward-propelling force of this bang was enough to counteract the contracting force of the gravity of all the matter in the universe without any need for a hypothetical cosmological constant.

I understand this (if I do) because in The Origin of the Universe it is given prominence and carefully explained. By contrast, in The Book of Universes it was almost lost in the flood of information and it was only because I’d read the earlier book that I grasped its importance.

The Book of Universes

Barrow gives a brisk recap of cosmology from the Sumerians and Egyptians, through the ancient Greeks’ establishment of the system named after Ptolemy in which the earth is the centre of the solar system, on through the revisions of Copernicus and Galileo which placed the sun firmly at the centre of the solar system, on to the three laws of Isaac Newton which showed how the forces which govern the solar system (and more distant bodies) operate.

There is then a passage on the models of the universe generated by the growing understanding of heat and energy acquired by Victorian physicists, which led to one of the most powerful models of the universe, the ‘heat death’ model popularised by Lord Kelvin in the 1850s, in which, in the far future, the universe evolves to a state of complete homegeneity, where no region is hotter than any other and therefore there is no thermodynamic activity, no life, just a low buzzing noise everywhere.

But this is all happens in the first 50 pages and is just preliminary throat-clearing before Barrow gets to the weird and wonderful worlds envisioned by modern cosmology i.e. from Einstein onwards.

In some of these models the universe expands indefinitely, in others it will reach a peak expansion before contracting back towards a Big Crunch. Some models envision a static universe, in others it rotates like a top, while other models are totally chaotic without any rules or order.

Some universes are smooth and regular, others characterised by clumps and lumps. Some are shaken by cosmic tides, some oscillate. Some allow time travel into the past, while others threaten to allow an infinite number of things to happen in a finite period. Some end with another big bang, some don’t end at all. And in only a few of them do the conditions arise for intelligent life to evolve.

The Book of Universes then goes on, in 12 chapters, to discuss – by my count – getting on for a hundred types or models of hypothetical universes, as conceived and worked out by mathematicians, physicists, astrophysicists and cosmologists from Einstein’s time right up to the date of publication, 2011.

A list of names

Barrow namechecks and briefly explains the models of the universe developed by the following (I am undertaking this exercise partly to remind myself of everyone mentioned, partly to indicate to you the overwhelming number of names and ideas the reader is bombarded with):

  • Aristotle
  • Ptolemy
  • Copernicus
  • Giovanni Riccioli
  • Tycho Brahe
  • Isaac Newton
  • Thomas Wright (1771-86)
  • Immanuel Kant (1724-1804)
  • Pierre Laplace (1749-1827) devised what became the standard Victorian model of the universe
  • Alfred Russel Wallace (1823-1913) discussed the physical conditions of a universe necessary for life to evolve in it
  • Lord Kelvin (1824-1907) material falls into the central region of the universe and coalesce with other stars to maintain power output over immense periods
  • Rudolf Clausius (1822-88) coined the word ‘entropy’ in 1865 to describe the inevitable progress from ordered to disordered states
  • William Jevons (1835-82) believed the second law of thermodynamics implies that universe must have had a beginning
  • Pierre Duhem (1961-1916) Catholic physicist accepted the notion of entropy but denied that it implied the universe ever had a beginning
  • Samuel Tolver Preson (1844-1917) English engineer and physicist, suggested the universe is so vast that different ‘patches’ might experience different rates of entropy
  • Ludwig Boltzmann and Ernst Zermelo suggested the universe is infinite and is already in a state of thermal equilibrium, but just with random fluctuations away from uniformity, and our galaxy is one of those fluctuations
  • Albert Einstein (1879-1955) his discoveries were based on insights, not maths: thus he saw the problem with Newtonian physics is that it privileges an objective outside observer of all the events in the universe; one of Einstein’s insights was to abolish the idea of a privileged point of view and emphasise that everyone is involved in the universe’s dynamic interactions; thus gravity does not pass through a clear, fixed thing called space; gravity bends space.

The American physicist John Wheeler once encapsulated Einstein’s theory in two sentences:

Matter tells space how to curve. Space tells matter how to move. (quoted on page 52)

  • Marcel Grossmann provided the mathematical underpinning for Einstein’s insights
  • Willem de Sitter (1872-1934) inventor of, among other things, the de Sitter effect which represents the effect of the curvature of spacetime, as predicted by general relativity, on a vector carried along with an orbiting body – de Sitter’s universe gets bigger and bigger for ever but never had a zero point; but then de Sitter’s model contains no matter
  • Vesto Slipher (1875-1969) astronomer who discovered the red shifting of distant galaxies in 1912, the first ever empirical evidence for the expansion of the galaxy
  • Alexander Friedmann (1888-1925) Russian mathematician who produced purely mathematical solutions to Einstein’s equation, devising models where the universe started out of nothing and expanded a) fast enough to escape the gravity exerted by its own contents and so will expand forever or b) will eventually succumb to the gravity of its own contents, stop expanding and contract back towards a big crunch. He also speculated that this process (expansion and contraction) could happen an infinite number of times, creating a cyclic series of bangs, expansions and contractions, then another bang etc
A graphic of the oscillating or cyclic universe (from Discovery magazine)

A graphic of the oscillating or cyclic universe (from Discovery magazine)

  • Arthur Eddington (1882-1944) most distinguished astrophysicist of the 1920s
  • George Lemaître (1894-1966) first to combine an expanding universe interpretation of Einstein’s equations with the latest data about redshifting, and show that the universe of Einstein’s equations would be very sensitive to small changes – his model is close to Eddington’s so that it is often called the Eddington-Lemaître universe: it is expanding, curved and finite but doesn’t have a beginning
  • Edwin Hubble (1889-1953) provided solid evidence of the redshifting (moving away) of distant galaxies, a main plank in the whole theory of a big bang, inventor of Hubble’s Law:
    • Objects observed in deep space – extragalactic space, 10 megaparsecs (Mpc) or more – are found to have a redshift, interpreted as a relative velocity away from Earth
    • This Doppler shift-measured velocity of various galaxies receding from the Earth is approximately proportional to their distance from the Earth for galaxies up to a few hundred megaparsecs away
  • Richard Tolman (1881-1948) took Friedmann’s idea of an oscillating universe and showed that the increased entropy of each universe would accumulate, meaning that each successive ‘bounce’ would get bigger; he also investigated what ‘lumpy’ universes would look like where matter is not evenly spaced but clumped: some parts of the universe might reach a maximum and start contracting while others wouldn’t; some parts might have had a big bang origin, others might not have
  • Arthur Milne (1896-1950) showed that the tension between the outward exploding force posited by Einstein’s cosmological constant and the gravitational contraction could actually be described using just Newtonian mathematics: ‘Milne’s universe is the simplest possible universe with the assumption that the universe s uniform in space and isotropic’, a ‘rational’ and consistent geometry of space – Milne labelled the assumption of Einsteinian physics that the universe is the same in all places the Cosmological Principle
  • Edmund Fournier d’Albe (1868-1933) posited that the universe has a hierarchical structure from atoms to the solar system and beyond
  • Carl Charlier (1862-1934) introduced a mathematical description of a never-ending hierarchy of clusters
  • Karl Schwarzschild (1873-1916) suggested  that the geometry of the universe is not flat as Euclid had taught, but might be curved as in the non-Euclidean geometries developed by mathematicians Riemann, Gauss, Bolyai and Lobachevski in the early 19th century
  • Franz Selety (1893-1933) devised a model for an infinitely large hierarchical universe which contained an infinite mass of clustered stars filling the whole of space, yet with a zero average density and no special centre
  • Edward Kasner (1878-1955) a mathematician interested solely in finding mathematical solutions to Einstein’s equations, Kasner came up with a new idea, that the universe might expand at different rates in different directions, in some parts it might shrink, changing shape to look like a vast pancake
  • Paul Dirac (1902-84) developed a Large Number Hypothesis that the really large numbers which are taken as constants in Einstein’s and other astrophysics equations are linked at a deep undiscovered level, among other things abandoning the idea that gravity is a constant: soon disproved
  • Pascual Jordan (1902-80) suggested a slight variation of Einstein’s theory which accounted for a varying constant of gravitation as through it were a new source of energy and gravitation
  • Robert Dicke (1916-97) developed an alternative theory of gravitation
  • Nathan Rosen (1909-995) young assistant to Einstein in America with whom he authored a paper in 1936 describing a universe which expands but has the symmetry of a cylinder, a theory which predicted the universe would be washed over by gravitational waves
  • Ernst Straus (1922-83) another young assistant to Einstein with whom he developed a new model, an expanding universe like those of Friedman and Lemaître but which had spherical holes removed like the bubbles in an Aero, each hole with a mass at its centre equal to the matter which had been excavated to create the hole
  • Eugene Lifschitz (1915-85) in 1946 showed that very small differences in the uniformity of matter in the early universe would tend to increase, an explanation of how the clumpy universe we live in evolved from an almost but not quite uniform distribution of matter – as we have come to understand that something like this did happen, Lifshitz’s calculations have come to be seen as a landmark
  • Kurt Gödel (1906-1978) posited a rotating universe which didn’t expand and, in theory, permitted time travel!
  • Hermann Bondi, Thomas Gold and Fred Hoyle collaborated on the steady state theory of a universe which is growing but remains essentially the same, fed by the creation of new matter out of nothing
  • George Gamow (1904-68)
  • Ralph Alpher and Robert Herman in 1948 showed that the ratio of the matter density of the universe to the cube of the temperature of any heat radiation present from its hot beginning is constant if the expansion is uniform and isotropic – they calculated the current radiation temperature should be 5 degrees Kelvin – ‘one of the most momentous predictions ever made in science’
  • Abraham Taub (1911-99) made a study of all the universes that are the same everywhere in space but can expand at different rates in different directions
  • Charles Misner (b.1932) suggested ‘chaotic cosmology’ i.e. that no matter how chaotic the starting conditions, Einstein’s equations prove that any universe will inevitably become homogenous and isotropic – disproved by the smoothness of the background radiation. Misner then suggested the Mixmaster universe, the  most complicated interpretation of the Einstein equations in which the universe expands at different rates in different directions and the gravitational waves generated by one direction interferes with all the others, with infinite complexity
  • Hannes Alfvén devised a matter-antimatter cosmology
  • Alan Guth (b.1947) in 1981 proposed a theory of ‘inflation’, that milliseconds after the big bang the universe underwent a swift process of hyper-expansion: inflation answers at a stroke a number of technical problems prompted by conventional big bang theory; but had the unforeseen implication that, though our region is smooth, parts of the universe beyond our light horizon might have grown from other areas of inflated singularity and have completely different qualities
  • Andrei Linde (b.1948) extrapolated that the inflationary regions might create sub-regions in  which further inflation might take place, so that a potentially infinite series of new universes spawn new universes in an ‘endlessly bifurcating multiverse’. We happen to be living in one of these bubbles which has lasted long enough for the heavy elements and therefore life to develop; who knows what’s happening in the other bubbles?
  • Ted Harrison (1919-2007) British cosmologist speculated that super-intelligent life forms might be able to develop and control baby universe, guiding the process of inflation so as to promote the constants require for just the right speed of growth to allow stars, planets and life forms to evolve. Maybe they’ve done it already. Maybe we are the result of their experiments.
  • Nick Bostrom (b.1973) Swedish philosopher: if universes can be created and developed like this then they will proliferate until the odds are that we are living in a ‘created’ universe and, maybe, are ourselves simulations in a kind of multiverse computer simulation

Although the arrival of Einstein and his theory of relativity marks a decisive break with the tradition of Newtonian physics, and comes at page 47 of this 300-page book, it seemed to me the really decisive break comes on page 198 with the publication Alan Guth’s theory of inflation.

Up till the Guth breakthrough, astrophysicists and astronomers appear to have focused their energy on the universe we inhabit. There were theoretical digressions into fantasies about other worlds and alternative universes but they appear to have been personal foibles and everyone agreed they were diversions from the main story.

Inflation

However, the idea of inflation, while it solved half a dozen problems caused by the idea of a big bang, seems to have spawned a literally fantastic series of theories and speculations.

Throughout the twentieth century, cosmologists grew used to studying the different types of universe that emerged from Einstein’s equations, but they expected that some special principle, or starting state, would pick out one that best described the actual universe. Now, unexpectedly, we find that there might be room for many, perhaps all, of these possible universes somewhere in the multiverse. (p.254)

This is a really massive shift and it is marked by a shift in the tone and approach of Barrow’s book. Up till this point it had jogged along at a brisk rate namechecking a steady stream of mathematicians, physicists and explaining how their successive models of the universe followed on from or varied from each other.

Now this procedure comes to a grinding halt while Barrow enters a realm of speculation. He discusses the notion that the universe we live in might be a fake, evolved from a long sequence of fakes, created and moulded by super-intelligences for their own purposes.

Each of us might be mannequins acting out experiments, observed by these super-intelligences. In which case what value would human life have? What would be the definition of free will?

Maybe the discrepancies we observe in some of the laws of the universe have been planted there as clues by higher intelligences? Or maybe, over vast periods of time, and countless iterations of new universes, the laws they first created for this universe where living intelligences could evolve have slipped, revealing the fact that the whole thing is a facade.

These super-intelligences would, of course, have computers and technology far in advance of ours etc. I felt like I had wandered into a prose version of The Matrix and, indeed, Barrow apologises for straying into areas normally associated with science fiction (p.241).

Imagine living in a universe where nothing is original. Everything is a fake. No ideas are ever new. There is no novelty, no originality. Nothing is ever done for the first time and nothing will ever be done for the last time… (p.244)

And so on. During this 15-page-long fantasy the handy sequence of physicists comes to an end as he introduces us to contemporary philosophers and ethicists who are paid to think about the problem of being a simulated being inside a simulated reality.

Take Robin Hanson (b.1959), a research associate at the Future of Humanity Institute of Oxford University who, apparently, advises us all that we ought to behave so as to prolong our existence in the simulation or, hopefully, ensure we get recreated in future iterations of the simulation.

Are these people mad? I felt like I’d been transported into an episode of The Outer Limits or was back with my schoolfriend Paul, lying in a summer field getting stoned and wondering whether dandelions were a form of alien life that were just biding their time till they could take over the world. Why not, man?

I suppose Barrow has to include this material, and explain the nature of the anthropic principle (p.250), and go on to a digression about the search for extra-terrestrial life (p.248), and discuss the ‘replication paradox’ (in an infinite universe there will be infinite copies of you and me in which we perform an infinite number of variations on our lives: what would happen if you came face to face with one of your ‘copies?? p.246) – because these are, in their way, theories – if very fantastical theories – about the nature of the universe and he his stated aim is to be completely comprehensive.

The anthropic principle

Observations of the universe must be compatible with the conscious and intelligent life that observes it. The universe is the way it is, because it has to be the way it is in order for life forms like us to evolve enough to understand it.

Still, it was a relief when he returned from vague and diffuse philosophical speculation to the more solid territory of specific physical theories for the last forty or so pages of the book. But it was very noticeable that, as he came up to date, the theories were less and less attached to individuals: modern research is carried out by large groups. And he increasingly is describing the swirl of ideas in which cosmologists work, which often don’t have or need specific names attached. And this change is denoted, in the texture of the prose, by an increase in the passive voice, the voice in which science papers are written: ‘it was observed that…’, ‘it was expected that…’, and so on.

  • Edward Tryon (b.1940) American particle physicist speculated that the entire universe might be a virtual fluctuation from the quantum vacuum, governed by the Heisenberg Uncertainty Principle that limits our simultaneous knowledge of the position and momentum, or the time of occurrence and energy, of anything in Nature.
  • George Ellis (b.1939) created a catalogue of ‘topologies’ or shapes which the universe might have
  • Dmitri Sokolov and Victor Shvartsman in 1974 worked out what the practical results would be for astronomers if we lived in a strange shaped universe, for example a vast doughnut shape
  • Yakob Zeldovich and Andrei Starobinsky in 1984 further explored the likelihood of various types of ‘wraparound’ universes, predicting the fluctuations in the cosmic background radiation which might confirm such a shape
  • 1967 the Wheeler-De Witt equation – a first attempt to combine Einstein’s equations of general relativity with the Schrödinger equation that describes how the quantum wave function changes with space and time
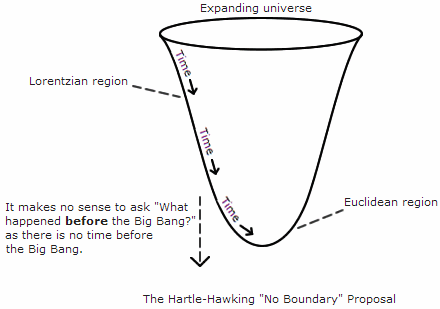
  • the ‘no boundary’ proposal – in 1982 Stephen Hawking and James Hartle used ‘an elegant formulation of quantum  mechanics introduced by Richard Feynman to calculate the probability that the universe would be found to be in a particular state. What is interesting is that in this theory time is not important; time is a quality that emerges only when the universe is big enough for quantum effects to become negligible; the universe doesn’t technically have a beginning because the nearer you approach to it, time disappears, becoming part of four-dimensional space. This ‘no boundary’ state is the centrepiece of Hawking’s bestselling book A Brief History of Time (1988). According to Barrow, the Hartle-Hawking model was eventually shown to lead to a universe that was infinitely large and empty i.e. not our one.
The Hartle-Hawking no boundary Hartle and Hawking No-Boundary Proposal

The Hartle-Hawking No-Boundary Proposal

  • In 1986 Barrow proposed a universe with a past but no beginning because all the paths through time and space would be very large closed loops
  • In 1997 Richard Gott and Li-Xin Li took the eternal inflationary universe postulated above and speculated that some of the branches loop back on themselves, giving birth to themselves
The self-creating universe of J.Richard Gott III and Li-Xin Li

The self-creating universe of J.Richard Gott III and Li-Xin Li

  • In 2001 Justin Khoury, Burt Ovrut, Paul Steinhardt and Neil Turok proposed a variation of the cyclic universe which incorporated strong theory and they called the ‘ekpyrotic’ universe, epkyrotic denoting the fiery flame into which each universe plunges only to be born again in a big bang. The new idea they introduced is that two three-dimensional universes may approach each other by moving through the additional dimensions posited by strong theory. When they collide they set off another big bang. These 3-D universes are called ‘braneworlds’, short for membrane, because they will be very thin
  • If a universe existing in a ‘bubble’ in another dimension ‘close’ to ours had ever impacted on our universe, some calculations indicate it would leave marks in the cosmic background radiation, a stripey effect.
  • In 1998 Andy Albrecht, João Maguijo and Barrow explored what might have happened if the speed of light, the most famous of cosmological constants, had in fact decreased in the first few milliseconds after the bang? There is now an entire suite of theories known as ‘Varying Speed of Light’ cosmologies.
  • Modern ‘String Theory’ only functions if it assumes quite a few more dimensions than the three we are used to. In fact some string theories require there to be more than one dimension of time. If there are really ten or 11 dimensions then, possibly, the ‘constants’ all physicists have taken for granted are only partial aspects of constants which exist in higher dimensions. Possibly, they might change, effectively undermining all of physics.
  • The Lambda-CDM model is a cosmological model in which the universe contains three major components: 1. a cosmological constant denoted by Lambda (Greek Λ) and associated with dark energy; 2. the postulated cold dark matter (abbreviated CDM); 3. ordinary matter. It is frequently referred to as the standard model of Big Bang cosmology because it is the simplest model that provides a reasonably good account of the following properties of the cosmos:
    • the existence and structure of the cosmic microwave background
    • the large-scale structure in the distribution of galaxies
    • the abundances of hydrogen (including deuterium), helium, and lithium
    • the accelerating expansion of the universe observed in the light from distant galaxies and supernovae

He ends with a summary of our existing knowledge, and indicates the deep puzzles which remain, not least the true nature of the ‘dark matter’ which is required to make sense of the expanding universe model. And he ends the whole book with a pithy soundbite. Speaking about the ongoing acceptance of models which posit a ‘multiverse’, in which all manner of other universes may be in existence, but beyond the horizon of where can see, he says:

Copernicus taught us that our planet was not at the centre of the universe. Now we may have to accept that even our universe is not at the centre of the Universe.

Reviews of other science books

Chemistry

Cosmology

The environment

Genetics and life

Human evolution

Maths

Particle physics

Psychology

1 Comment
by Simon on April 10, 2019  •  Permalink
Posted in Books, Cosmology, Science
Tagged , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , ,

Posted by Simon on April 10, 2019

https://astrofella.wordpress.com/2019/04/10/the-book-of-universes-john-d-barrow/

Alex’s Adventures In Numberland by Alex Bellos (2010)

Alexander Bellos (born in 1969) is a British writer and broadcaster. He is the author of books about Brazil and mathematics, as well as having a column in The Guardian newspaper. After adventures in Brazil (see his Wikipedia page) he returned to England in 2007 and wrote this, his first book. It spent four months in the Sunday Times bestseller list and led on to five more popular maths books.

It’s a hugely enjoyable read for three reasons:

  1. Bellos immediately establishes a candid, open, good bloke persona, sharing stories from his early job as a reporter on the Brighton Argus, telling some colourful anecdotes about his time in Brazil and then being surprisingly open about the way that, when he moved back to Britain, he had no idea what to do. The tone of the book is immediately modern, accessible and friendly.
  2. However this doesn’t mean he is verbose. The opposite. The book is packed with fascinating information. Every single paragraph, almost every sentence contains a fact or insight which makes you sit up and marvel. It is stufffed with good things.
  3. Lastly, although its central theme is mathematics, it approaches this through a wealth of information from the humanities. There is as much history and psychology and anthropology and cultural studies and philosophy as there is actual maths, and these are all subjects which the average humanities graduate can immediately relate to and assimilate.

Chapter Zero – A Head for Numbers

Alex meets Pierre Pica, a linguist who’s studied the Munduruku people of the Amazon and discovered they have little or no sense of numbers. They only have names for numbers up to five. Also, they cluster numbers together logarithmically i.e. the higher the number, the closer together they clustered them. Same thing is done by kindergarten children who only slowly learn that numbers are evenly spaced, in a linear way.

This may be because small children and the Munduruku don’t count so much as estimate using the ratios between numbers.

It may also be because above a certain number (five) Stone Age man needed to make quick estimates along the lines of, Are there more wild animals / members of the other gang, than us?

Another possibility is that distance appears to us to be logarithmic due to perspective: the first fifty yards we see in close detail, the next fifty yards not so detailed, beyond 100 yards looking smaller, and so on.

It appears that we have to be actively taught when young to overcome our logarithmic instincts, and to apply the rule that each successive whole number is an equal distance from its predecessor and successor i.e. the rational numbers lies along a straight line at regular intervals.

More proof that the logarithmic approach is the deep, hard-wired one is the way most of us revert to its perspective when considering big numbers. As John Allen Paulos laments, people make no end of fuss about discrepancies between 2 or 3 or 4 – but are often merrily oblivious to the difference between a million or a billion, let alone a trillion. For most of us these numbers are just ‘big’.

He goes on to describe experiments done on chimpanzees, monkeys and lions which appear to show that animals have the ability to estimate numbers. And then onto experiments with small babies which appear to show that as soon as they can focus on the outside world, babies can detect changes in number of objects.

And it appears that we also have a further number skill, that guesstimating things – the journey takes 30 or 40 minutes, there were twenty or thirty people at the party, you get a hundred, maybe hundred and fifty peas in a sack. When it comes to these figures almost all of us give rough estimates.

To summarise:

  • we are sensitive to small numbers, acutely so of 1, 2, 3, 4, less so of 5, 6, 7, 8, 9
  • left to our own devices we think logarithmically about larger numbers i.e lose the sense of distinction between them, clump them together
  • we have a good ability to guesstimate medium size numbers – 30, 40, 100

But it was only with the invention of notation, a way of writing numbers down, that we were able to create the linear system of counting (where every number is 1 larger than its predecessor, laid out in a straight line, at regular intervals).

And that this cultural invention enabled human beings to transcend our vague guesstimating abilities, and laid the basis for the systematic manipulation of the world which followed

Chapter One – The Counter Culture

The probable origins of counting lie in stock taking in the early agricultural revolution some 8,000 years ago.

We nowadays count using a number base 10 i.e. the decimal system. But other bases have their virtues, especially base 12. It has more factors i.e. is easier to divide: 12 can be divided neatly by 2, 3, 4 and 6. A quarter of 10 is 2.5 but of 12 is 3. A third of 10 is 3.333 but of 12 is 4. Striking that a version of the duodecimal system (pounds, shillings and pence) hung on in Britain till we finally went metric in the 1970s. There is even a Duodecimal Society of America which still actively campaigns for the superiority of a base 12 counting scheme.

Bellos describes a bewildering variety of other counting systems and bases. In 1716 King Charles XII of Sweden asked Emmanuel Swedenborg to devise a new counting system with a base of 64. The Arara in the Amazon count in pairs, the Renaissance author Luca Paccioli was just one of hundreds who have devised finger-based systems of counting – indeed, the widespread use of base 10 probably stems from the fact that we have ten fingers and toes.

He describes a complicated Chinese system where every part of the hand and fingers has a value which allows you to count up to nearly a billion – on one hand!

The Yupno system which attributes a different value for parts of the body up to its highest number, 33, represented by the penis.

Diagram showing numbers attributed to parts of the body by the Yupno tribe

Diagram showing numbers attributed to parts of the body by the Yupno tribe

There’s another point to make about his whole approach which comes out if we compare him with the popular maths books by John Allen Paulos which I’ve just read.

Paulos clearly sees the need to leaven his explanations of comparative probability and Arrow’s Theorem and so on with lighter material and so his strategy is to chuck into his text things which interest him: corny jokes, anecdotes about baseball, casual random digressions which occur to him in mid-flow. But al his examples clearly 1. emanate from Paulos’s own interests and hobby horses (especially baseball) and 2. they are tacked onto the subjects being discussed.

Bellos, also, has grasped that the general reader needs to be spoonfed maths via generous helpings of other, more easily digestible material. But Bellos’s choice of material arises naturally from the topic under discussion. The humour emerges naturally and easily from the subject matter instead of being tacked on in the form of bad jokes.

You feel yourself in the hands of a master storyteller who has all sorts of wonderful things to explain to you.

In fourth millennium BC, an early counting system was created by pressing a reed into soft clay. By 2700 BC the Sumerians were using cuneiform. And they had number symbols for 1, 10, 60 and 3,600 – a mix of decimal and sexagesimal systems.

Why the Sumerians grouped their numbers in 60s has been described as one of the greatest unresolved mysteries in the history of arithmetic. (p.58)

Measuring in 60s was inherited by the Babylonians, the Egyptians and the Greeks and is why we still measure hours in 60 minutes and the divisions of a circle by 360 degrees.

I didn’t know that after the French Revolution, when the National Convention introduced the decimal system of weights and measures, it also tried to decimalise time, introducing a new system whereby every day would be divided into ten hours, each of a hundred minutes, each divided into 100 seconds. Thus there were a very neat 10 x 100 x 100 = 100,000 seconds in a day. But it failed. An hour of 60 minutes turns out to be a deeply useful division of time, intuitively measurable, and a reasonable amount of time to spend on tasks. The reform was quietly dropped after six months, although revolutionary decimal clocks still exist.

Studies consistently show that Chinese children find it easier to count than European children. This may be because of our system of notation, or the structure of number names. Instead of eleven or twelve, Chinese, Japanese and Koreans say the equivalent of ten one, ten two. 21 and 22 become two ten one and two ten two. It has been shown that this makes it a lot simpler and more intuitive to do basic addition and subtraction.

Bellos goes on to describe the various systems of abacuses which have developed in different cultures, before explaining the phenomenal popularity of abacus counting, abacus clubs, and abacus championships in Japan which helps kids develop the ability to perform anzan, using the mental image of an abacus to help its practitioners to sums at phenomenal speed.

Chapter Two – Behold!

The mystical sense of the deep meaning of numbers, from Pythagoras with his vegetarian religious cult of numbers in 4th century BC Athens to Jerome Carter who advises leading rap stars about the numerological significance of their names.

Euclid and the elegant and pure way he deduced mathematical theorems from a handful of basic axioms.

A description of the basic Platonic shapes leads into the nature of tessalating tiles, and the Arab pioneering of abstract design. The complex designs of the Sierpinski carpet and the Menger sponge. And then the complex and sophisticated world of origami, which has its traditionalists, its pioneers and surprising applications to various fields of advanced science, introducing us to the American guru of modern origami, Robert Lang, and the Japanese rebel, Kazuo Haga, father of Haga’s Theorem.

Chapter Three – Something About Nothing

A bombardment of information about the counting systems of ancient Hindus, Buddhists, about number symbols in Sanskrit, Hebrew, Greek and Latin. How the concept of zero was slowly evolved in India and moved to the Muslim world with the result that the symbols we use nowadays are known as the Arabic numerals.

A digression into ‘a set of arithmetical tricks known as Vedic Mathematics ‘ devised by a young Indian swami at the start of the twentieth century, Bharati Krishna Tirthaji, based on a series of 16 aphorisms which he found in the ancient holy texts known as the Vedas.

Shankaracharya is a commonly used title of heads of monasteries called mathas in the Advaita Vedanta tradition. Tirthaji was the Shankaracharya of the monastery at Puri. Bellos goes to visit the current Shankaracharya who explains the closeness, in fact the identity, of mathematics and Hindu spirituality.

Chapter Four – Life of Pi

An entire chapter about pi which turns out not only to be a fundamental aspect of calculating radiuses and diameters and volumes of circles and cubes, but also to have a long history of mathematicians vying with each other to work out its value to as many decimal places as possible (we currently know the value of pi to 2.7 trillion decimal places) and the surprising history of people who have set records reciting the value if pi.

Thus, in 2006, retired Japanese engineer Akira Haraguchi set a world record for reciting the value of pi to the first 100,000 decimal places from memory! It took 16 hours with five minute beaks every two hours to eat rice balls and drink some water.

There are several types or classes of numbers:

  • natural numbers – 1, 2, 3, 4, 5, 6, 7…
  • integers – all the natural numbers, but including the negative ones as well – …-3, -2, -1, 0, 1, 2, 3…
  • fractions
  • which are also called rational numbers
  • numbers which cannot be written as fractions are called irrational numbers
  • transcendent numbers – ‘a transcendental number is an irrational number that cannot be described by an equation with a finite number of terms’

The qualities of the heptagonal 50p coin and the related qualities of the Reuleux triangle.

Chapter Five – The x-factor

The origin of algebra (in Arab mathematicians).

Bellos makes the big historical point that for the Greeks (Pythagoras, Plato, Euclid) maths was geometric. They thought of maths as being about shapes – circles, triangles, squares and so on. These shapes had hidden properties which maths revealed, thus giving – the Pythagoreans thought – insight into the secret deeper values of the world.

It is only with the introduction of algebra in the 17th century (Bellos attributes its widespread adoption to Descartes’s Method in the 1640s) that it is possible to fly free of shapes into whole new worlds of abstract numbers and formulae.

Logarithms turn the difficult operation of multiplication into the simpler operation of addition. If X x Y = Z, then log X + log Y = log Z. They were invented by a Scottish laird John Napier, and publicised in a huge book of logarithmic tables published in 1614. Englishman Henry Briggs established logarithms to base 10 in 1628. In 1620 Englishman Edmund Gunter marked logarithms on a ruler. Later in the 1620s Englishman William Oughtred placed two logarithmic rulers next to each other to create the slide rule.

Three hundred years of dominance by the slide rule was brought to a screeching halt by the launch of the first pocket calculator in 1972.

Quadratic equations are equations with an x and an x², e.g. 3x² + 2x – 4 = 0. ‘Quadratics have become so crucial to the understanding of the world, that it is no exaggeration to say that they underpin modern science’ (p.200).

Chapter Six – Playtime

Number games. The origin of Sudoku, which is Japanese for ‘the number must appear only once’. There are some 5 billion ways for numbers to be arranged in a table of nine cells so that the sum of any row or column is the same.

There have, apparently, only been four international puzzle crazes with a mathematical slant – the tangram, the Fifteen puzzle, Rubik’s cube and Sudoku – and Bellos describes the origin and nature and solutions to all four. More than 300 million cubes have seen sold since Ernö Rubik came up with the idea in 1974. Bellos gives us the latest records set in the hyper-competitive sport of speedcubing: the current record of restoring a copletely scrambled cube to order (i.e. all the faces of one colour) is 7.08 seconds, a record held by Erik Akkersdijk, a 19-year-old Dutch student.

A visit to the annual Gathering for Gardner, honouring Martin Gardner, one of the greatest popularisers of mathematical games and puzzles who Bellos visits. The origin of the ambigram, and the computer game Tetris.

Chapter Seven – Secrets of Succession

The joy of sequences. Prime numbers.

The fundamental theorem of arithmetic – In number theory, the fundamental theorem of arithmetic, also called the unique factorization theorem or the unique-prime-factorization theorem, states that every integer greater than 1 either is a prime number itself or can be represented as the product of prime numbers.

The Goldbach conjecture – one of the oldest and best-known unsolved problems in number theory and all of mathematics. It states that, Every even integer greater than 2 can be expressed as the sum of two primes. The conjecture has been shown to hold for all integers less than 4 × 1018, but remains unproven despite considerable effort.

Neil Sloane’s idea of persistence – The number of steps it takes to get to a single digit by multiplying all the digits of the preceding number to obtain a second number, then multiplying all the digits of that number to get a third number, and so on until you get down to a single digit. 88 has a persistence of three.

88 → 8 x 8 = 64 → 6 x 4 = 24 → 2 x 4 = 8

John Horton Conway’s idea of the powertrain – For any number abcd its powertrain goes to abcd, in the case of numbers with an odd number of digits the final one has no power, abcde’s powertrain is abcde.

The Recamán sequence Subtract if you can, unless a) it would result in a negative number or b) the number is already in the sequence. The result is:

0, 1, 3, 6, 2, 7, 13, 20, 12, 21, 11….

Gijswijt’s sequence a self-describing sequence where each term counts the maximum number of repeated blocks of numbers in the sequence immediately preceding that term.

1, 1, 2, 1, 1, 2, 2, 2, 3, 1, 1, 2, 1, 1, 2, 2, 2, 3, 2, 1, …

Perfect number A perfect number is any number that is equal to the sum of its factors. Thus 6 – its factors (the numbers which divided into it) are 1, 2 and 3. Which also add up to (are the sum of) 6. The next perfect number is 28 because its factors – 1, 2, 4, 7, 14 – add up to 28. And so on.

Amicable numbers A number is amicable if the sum of the factors of the first number equals the second number, and if the sum of the factors of the second number equals the first. The factors of 220 are 1, 2, 4, 5, 10, 11, 20, 22, 44, 55 and 110. Added together these make 284. The factors of 284 are 1, 2, 4, 71 and 142. Added together they make 220!

Sociable numbers In 1918 Paul Poulet invented the term sociable numbers. ‘The members of aliquot cycles of length greater than 2 are often called sociable numbers. The smallest two such cycles have length 5 and 28’

Mersenne’s prime A prime number which can be written in the form 2n – 1 a prime number that is one less than a power of two. That is, it is a prime number of the form Mn = 2n − 1 for some integer n. The exponents n which give Mersenne primes are 2, 3, 5, 7, 13, 17, 19, 31, … and the resulting Mersenne primes are 3, 7, 31, 127, 8191, 131071, 524287, 2147483647, …

These and every other sequence ever created by humankind are documented on The On-Line Encyclopedia of Integer Sequences (OEIS), also cited simply as Sloane’s. This is an online database of integer sequences, created and maintained by Neil Sloane while a researcher at AT&T Labs.

Chapter Eight – Gold Finger

The golden section a number found by dividing a line into two parts so that the longer part divided by the smaller part is also equal to the whole length divided by the longer part.

Phi The number is often symbolized using phi, after the 21st letter of the Greek alphabet. In an equation form:

a/b = (a+b)/a = 1.6180339887498948420 …

As with pi (the ratio of the circumference of a circle to its diameter), the digits go on and on, theoretically into infinity. Phi is usually rounded off to 1.618.

The Fibonnaci sequence Each number in the sequence is the sum of the two numbers that precede it. So the sequence goes: 0, 1, 1, 2, 3, 5, 8, 13, 21, 34, and so on. The mathematical equation describing it is Xn+2= Xn+1 + Xn.

as the basis of seeds in flowerheads, arrangement of leaves round a stem, design of nautilus shell and much more.

Chapter Nine – Chance Is A Fine Thing

A chapter about probability and gambling.

Impossibility has a value 0, certainty a value 1, everything else is in between. Probabilities can be expressed as fractions e.g. 1/6 chance of rolling a 6 on a die, or as percentages, 16.6%, or as decimals, 0.16…

The probability is something not happening is 1 minus the probability of that thing happening.

Probability was defined and given mathematical form in 17th century. One contribution was the questions the Chevalier de Méré asked the mathematical prodigy Blaise Pascal. Pascal corresponded with his friend, Pierre de Fermat, and they worked out the bases of probability theory.

Expected value is what you can expect to get out of a bet. Bellos takes us on a tour of the usual suspects – rolling dice, tossing coins, and roulette (invented in France).

Payback percentage if you bet £10 at craps, you can expect – over time – to receive an average of about £9.86 back. In other words craps has a payback percentage of 98.6 percent. European roulette has a payback percentage of 97.3 percent. American roulette, 94.7 percent. On other words, gambling is a fancy way of giving your money away. A miserly slot machine has a payback percentage of 85%. The National Lottery has a payback percentage of 50%.

The law of large numbers The more you play a game of chance, the more likely the results will approach the statistical probability. Toss a coin three times, you might get three heads. Toss a coin a thousand times, the chances are you will get very close the statistical probability of 50% heads.

The law of very large numbers With a large enough sample, outrageous coincidences become likely.

The gambler’s fallacy The mistaken belief that, if something happens more frequently than normal during a given period, it will happen less frequently in the future (or vice versa). In other words, that a random process becomes less random, and more predictable, the more it is repeated.

The birthday paradox The probability that, in a set of n randomly chosen people, some pair of them will have the same birthday. By the pigeonhole principle, the probability reaches 100% when the number of people reaches 367 (since there are only 366 possible birthdays, including February 29). However, 99.9% probability is reached with just 70 people, and 50% probability with 23 people. (These conclusions are based on the assumption that each day of the year (excluding February 29) is equally probable for a birthday.) In other words you only need a group of 23 people to have an evens chance that two of them share a birthday.

The drunkard’s walk

The difficulty of attaining true randomness and the human addiction to finding meaning in anything.

The distinction between playing strategy (best strategy to win a game) and betting strategy (best strategy to maximise your winnings), not always the same.

Chapter Ten – Situation Normal

Carl Friedrich Gauss, the bell curve, normal distribution aka Gaussian distribution. Normal or Gaurrian distribution results in a bell curve. Bellos describes the invention and refinement of the bell curve (he explains that ‘the long tail’ results from a mathematician who envisioned a thin bell curve as looking like two kangaroos facing each other with their long tails heading off in opposite directions). And why

Regression to the mean – if the outcome of an event is determined at least in part by random factors, then an extreme event will probably be followed by one that is less extreme. And recent devastating analyses which show how startlingly random sports achievements are, from leading baseball hitters to Simon Kuper and Stefan Szymanski’s analysis of the form of the England soccer team.

Chapter Eleven – The End of the Line

Two breakthroughs which paved the way for modern i.e. 20th century, maths: the invention of non-Euclidean geometry, specifically the concept of hyperbolic geometry. To picture this draw a triangle on a Pringle. it is recognisably a triangle but all its angles do not add up to 180°, therefore it defies, escapes, eludes all the rule of Euclidean geometry, which were designed for flat 2D surfaces.

Bellos introduces us to Daina Taimina, a maths prof at Cornell University, who invented a way of crocheting hyperbolic surfaces. The result looks curly, like curly kale or the surface of coral.

Anyway, the breakaway from flat 2-D Euclidean space led to theories about curved geometry, either convex like a sphere, or hyperbolic like the pringle. It was this notion of curved space, which paved the way for Einstein’s breakthrough ideas in the early 20th century.

The second big breakthrough was Georg Cantor’s discovery that you can have many different types of infinity. Until Cantor the mathematical tradition from the ancient Greeks to Galileo and Newton had fought shy of infinity which threatened to disrupt so many formulae.

Cantor’s breakthrough was to stop thinking about numbers, and instead think of sets. This is demonstrated through the paradoxes of Hilbert’s Hotel. You need to buckle your safety belt to understand it.

Thoughts

This is easily the best book about maths I’ve ever read. It gives you a panoramic history of the subject which starts with innumerate cavemen and takes us to the edge of Einstein’s great discoveries. But Bellos adds to it all kinds of levels and abilities.

He is engaging and candid and funny. He is fantastically authoritative, taking us gently into forests of daunting mathematical theory without placing a foot wrong. He’s a great explainer. He knows a good story when he sees one, and how to tell it engagingly. And in every chapter there is a ‘human angle’ as he describes his own personal meetings and interviews with many of the (living) key players in the world of contemporary maths, games and puzzles.

Like the Ian Stewart book but on a vastly bigger scale, Bellos makes you feel what it is like to be a mathematician, not just interested in nature’s patterns (the basis of Stewart’s book, Nature’s Numbers) but in the beauty of mathematical theories and discoveries for their own sakes. (This comes over very strongly in chapter seven with its description of some of the weirdest and wackiest number sequences dreamed up by the human mind.) I’ve often read scientists describing the beauty of mathematical theories, but Bellos’s book really helps you develop a feel for this kind of beauty.

For me, I think three broad conclusions emerged:

1. Most mathematicians are in it for the fun. Setting yourself, and solving, mathematical puzzles is obviously extremely rewarding. Maths includes the vast territory of puzzles and games, such as the Sudoku and so on he describes in chapter six. Obviously it has all sorts of real-world application in physics, engineering and so on, but Bellos’s book really brings over that a true understanding of maths begins in puzzles, games and patterns, and often remains there for a lifetime. Like everything else maths is no highly professionalised the property of tenured professors in universities; and yet even to this day – as throughout its history – contributions can be made by enthusiastic amateurs.

2. As he points out repeatedly, many insights which started out as the hobby horses of obsessives, or arcane breakthroughs on the borders of our understanding, and which have been airily dismissed by the professionals, often end up being useful, having applications no-one dreamed of. Either they help unravel aspects of the physical universe undreamed of when they were discovered, or have been useful to human artificers. Thus the development of random number sequences seemed utterly pointless in the 19th century, but now underlies much internet security.

On a profounder note, Bellos expresses the eerie, mystical sense many mathematicians have that it seems so strange, so pregnant with meaning, that so many of these arcane numbers end up explaining aspects of the world their inventors knew nothing of. Ian Stewart has an admirably pragmatic explanation for this: he speculates that nature uses everything it can find in order to build efficient life forms. Or, to be less teleological, over the past 3 and a half billion years, every combination of useful patterns has been tried out. Given this length of time, and the incalculable variety of life forms which have evolved on this planet, it would be strange if every number system conceivable by one of those life forms – humankind – had not been tried out at one time or another.

3. My third conclusion is that, despite John Allen Paulos’s and Bellos’s insistence, I do not live in a world ever-more bombarded by maths. I don’t gamble on anything, and I don’t follow sports – the two biggest popular areas where maths is important – and the third is the twin areas of surveys and opinion polls (55% of Americans believe in alien abductions etc etc) and the daily blizzard of reports (for example, I see in today’s paper that the ‘Number of primary school children at referral units soars’).

I register their existence but they don’t impact on me for the simple reason that I don’t believe any of them. In 1992 every opinion poll said John Major would lose the general election, but he won with a thumping majority. Since then I haven’t believed any poll about anything. For example almost all the opinion polls predicted a win for Remain in the Brexit vote. Why does any sane person believe opinion polls?

And ‘new and shocking’ reports come out at the rate of a dozen a day and, on closer examination, lots of them turn out to be recycled information, or much much more mundane releases of data sets from which journalists are paid to draw the most shocking and extreme conclusions. Some may be of fleeting interest but once you really grasp that the people reporting them to you are paid to exaggerate and horrify, you soon learn to ignore them.

If you reject or ignore these areas – sport, gambling and the news (made up of rehashed opinion polls, surveys and reports) – then unless you’re in a profession which actively requires the sophisticated manipulation of figures, I’d speculate that most of the rest of us barely come into contact with numbers from one day to the next.

I think that’s the answer to Paulos and Bellos when they are in their ‘why aren’t more people mathematically numerate?’ mode. It’s because maths is difficult, and counter-intuitive, and hard to understand and follow, it is a lot of work, it does make your head ache. Even trying to solve a simple binomial equation hurt my brain.

But I think the biggest reason that ‘we’ are so innumerate is simply that – beautiful, elegant, satisfying and thought-provoking though maths may be to the professionals – maths is more or less irrelevant to most of our day to day lives, most of the time.

Related links

Reviews of other science books

Chemistry

Cosmology

The Environment

Genetics and life

Human evolution

Maths

Particle physics

Psychology

Leave a comment
by Simon on April 1, 2019  •  Permalink
Posted in Books, History, Mathematics
Tagged , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , ,

Posted by Simon on April 1, 2019

https://astrofella.wordpress.com/2019/04/01/alexs-adventures-in-numberland-alex-bellos/